Soma de Riemann

A soma de Riemann é um método fundamental na teoria da integral, utilizado para aproximar a área sob uma curva. É especialmente útil em cálculo multivariável.

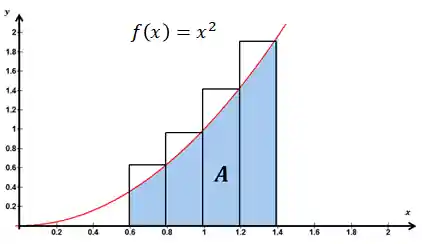
Definição e Intuição

A soma de Riemann consiste em dividir o domínio de integração em subintervalos pequenos e calcular a soma das áreas dos retângulos formados por esses subintervalos. A ideia é que, à medida que os subintervalos se tornam mais finos, a soma dessas áreas se aproxima cada vez mais da área real sob a curva.

Funções de Uma Variável

Para uma função $f (x)$ definida em um intervalo $[a, b]$ , a soma de Riemann pode ser expressa como:

\sum_{i = 1}^{n} f (x_{i}^{*}) Δ x

onde:

$Δ x = \frac{b - a}{n}$ é o comprimento do subintervalo,
$x_{i}^{*}$ é um ponto no $i$ -ésimo subintervalo.

Exemplo:

Considere a função $f (x) = x^{2}$ em $[0, 1]$ . Dividamos este intervalo em 4 subintervalos iguais:

Δ x = \frac{1 - 0}{4} = 0.25

Os pontos de divisão são: $x_{1} = 0.25$ , $x_{2} = 0.5$ , $x_{3} = 0.75$ , e $x_{4} = 1$ . Se escolhemos os pontos médios como $x_{i}^{*}$ , temos:

$f (0.125) = 0.015625$
$f (0.375) = 0.140625$
$f (0.625) = 0.390625$
$f (0.875) = 0.765625$

A soma de Riemann é:

S_{4} = \sum_{i = 1}^{4} f (x_{i}^{*}) Δ x = (0.015625 + 0.140625 + 0.390625 + 0.765625) \cdot 0.25 = 0.3125

Funções de Duas Variáveis

Para funções de duas variáveis, a soma de Riemann é estendida para volumes sob superfícies em $R^{3}$ . Considere uma função $f (x, y)$ definida sobre um retângulo $[a, b] \times [c, d]$ .

A soma de Riemann pode ser escrita como:

\sum_{i = 1}^{m} \sum_{j = 1}^{n} f (x_{i}^{*}, y_{j}^{*}) Δ x Δ y

onde:

$Δ x = \frac{b - a}{m}$ e $Δ y = \frac{d - c}{n}$ são os comprimentos dos subintervalos,
$(x_{i}^{*}, y_{j}^{*})$ é um ponto no $i$ -ésimo subintervalo em $x$ e $j$ -ésimo subintervalo em $y$ .

Exemplo:

Considere a função $f (x, y) = x y$ sobre o retângulo $[0, 1] \times [0, 1]$ . Dividamos este retângulo em 4 subretângulos iguais:

Δ x = \frac{1 - 0}{2} = 0.5, Δ y = \frac{1 - 0}{2} = 0.5

Os pontos de divisão são: $x_{1} = 0.25$ , $x_{2} = 0.75$ e $y_{1} = 0.25$ , $y_{2} = 0.75$ . Se escolhemos os pontos médios como $(x_{i}^{*}, y_{j}^{*})$ , temos:

$f (0.375, 0.375) = 0.140625$
$f (0.875, 0.375) = 0.328125$
$f (0.375, 0.875) = 0.328125$
$f (0.875, 0.875) = 0.765625$

A soma de Riemann é:

S_{4} = \sum_{i = 1}^{2} \sum_{j = 1}^{2} f (x_{i}^{*}, y_{j}^{*}) Δ x Δ y = (0.140625 + 0.328125 + 0.328125 + 0.765625) \cdot 0.25 \cdot 0.25 = 0.1875

Esses exemplos ilustram como a soma de Riemann pode ser aplicada tanto para funções de uma variável quanto para funções de duas variáveis, aproximando áreas e volumes respectivamente.