Método Gráfico

O método gráfico é uma técnica fundamental no cálculo numérico utilizado para localizar os zeros de uma função. Este método envolve a representação visual da função através do desenho de seu gráfico, permitindo identificar pontos onde a função corta o eixo das abscissas (eixo x).

Passos para Aplicar o Método Gráfico

1. Definição da Função:
   Considere uma função $f(x)$ que deseja encontrar os zeros.

2. Escolha do Intervalo:
   Escolha um intervalo de valores para $x$ onde a função pode ter zeros. Por exemplo, se estiver trabalhando com a função $f(x)=x^3-2x+1$, pode escolher o intervalo $[-2,2]$.

3. Criação do Gráfico:
   Use um software de gráficos ou papel e lápis para desenhar o gráfico da função no intervalo escolhido. Por exemplo:

   • Para a função $f(x)=x^3-2x+1$, você pode calcular alguns pontos para traçar o gráfico, como $f(-2)=-5$, $f(-1)=2$, $f(0)=1$, $f(1)=0$, e $f(2)=7$.

4. Identificação dos Zeros:
   Os zeros da função são os valores de $x$ onde o gráfico corta o eixo x, ou seja, onde $f(x)=0$. No exemplo acima, você pode observar que a função corta o eixo x em $x=1$, indicando que um zero é $x=1$.

5. Refinamento:
   Para encontrar zeros com maior precisão, você pode refinar o intervalo onde os zeros são localizados. Por exemplo, se você suspeita que há outro zero entre $0$ e $2$, você pode desenhar o gráfico nesse novo intervalo para identificar a posição exata.

Exemplo Prático

Considere a função $f(x)=x^3-4x+1$. Para aplicar o método gráfico:

• Passo 1: Defina a função.
• Passo 2: Escolha um intervalo, por exemplo, $[-2,2]$.
• Passo 3: Crie o gráfico. Calcule alguns pontos:
  • $f(-2)=(-2{)}^3-4(-2)+1=-8+8+1=1$
  • $f(-1)=(-1{)}^3-4(-1)+1=-1+4+1=4$
  • $f(0)=0^3-4(0)+1=1$
  • $f(1)=1^3-4(1)+1=1-4+1=-2$
  • $f(2)=2^3-4(2)+1=8-8+1=1$
• Passo 4: Identifique os zeros. No intervalo escolhido, o gráfico corta o eixo x entre $x=0$ e $x=1$, indicando que há um zero nesse intervalo.
• Passo 5: Refine o intervalo para encontrar a posição exata do zero.

Método Gráfico Aplicado ao Formato $f(x)-g(x)$

O método gráfico pode ser aplicado para encontrar os zeros de uma função que é a diferença entre duas funções, $f(x)-g(x)$. Este método é particularmente útil quando as funções envolvidas são complexas ou não podem ser resolvidas analiticamente.

Passos para Aplicar o Método Gráfico

1. Definição das Funções:
   Considere duas funções $f(x)$ e $g(x)$. Os zeros da função $h(x)=f(x)-g(x)$ são os valores de $x$ onde o gráfico de $h(x)$ corta o eixo x, ou seja, onde $h(x)=0$.

2. Escolha do Intervalo:
   Escolha um intervalo de valores para $x$ onde a função $h(x)=f(x)-g(x)$ pode ter zeros. Por exemplo, se estiver trabalhando com as funções $f(x)=x^3-2x+1$ e $g(x)=x^2-1$, pode escolher o intervalo $[-2,2]$.

3. Criação do Gráfico:
   Use um software de gráficos ou papel e lápis para desenhar o gráfico da função $h(x)=f(x)-g(x)$ no intervalo escolhido.

4. Identificação dos Zeros:
   Os zeros da função $h(x)$ são os valores de $x$ onde o gráfico corta o eixo x, ou seja, onde $h(x)=0$. No exemplo acima, você pode observar que a função corta o eixo x em $x=1$, indicando que um zero é $x=1$.

5. Refinamento:
   Para encontrar zeros com maior precisão, você pode refinar o intervalo onde os zeros são localizados. Por exemplo, se você suspeita que há outro zero entre $0$ e $2$, você pode desenhar o gráfico nesse novo intervalo para identificar a posição exata.

Exemplo Prático

Considere as funções $f(x)=x^3-2x+1$ e $g(x)=x^2-1$. Para aplicar o método gráfico:

• Passo 1: Defina as funções.
• Passo 2: Escolha um intervalo, por exemplo, $[-2,2]$.
• Passo 3: Crie o gráfico de $h(x)=f(x)-g(x)$:
  • $h(-2)=-5$
  • $h(-1)=2$
  • $h(0)=2$
  • $h(1)=0$
  • $h(2)=2$
• Passo 4: Identifique os zeros do gráfico de $h(x)$, que neste caso é $x=1$.

Código Python

Aqui está o código completo:

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    """Function f(x) = x^3 - 2x + 1."""
    return x**3 - 2*x + 1

def g(x):
    """Function g(x) = x^2 - 1."""
    return x**2 - 1

def plot_graphical_method(f, g, x_range=(-2, 2), num_points=1000):
    """
    Plot f(x), g(x), and h(x) = f(x) - g(x) over a specified range and mark the zeros of h(x).

    Parameters:
    f, g      -- Functions to plot
    x_range   -- Tuple (min, max) for x-axis
    num_points-- Number of points in the plot
    """
    x = np.linspace(x_range[0], x_range[1], num_points)
    h = f(x) - g(x)

    plt.plot(x, f(x), label='f(x) = x^3 - 2x + 1')
    plt.plot(x, g(x), label='g(x) = x^2 - 1')
    plt.plot(x, h, label='h(x) = f(x) - g(x)')
    plt.axhline(0, color='gray', linestyle='--')

    # Find approximate zeros of h(x) using sign changes
    zero_indices = np.where(np.diff(np.sign(h)))[0]
    zeros = []
    for idx in zero_indices:
        # Linear interpolation for a better zero estimate
        x0, x1 = x[idx], x[idx+1]
        y0, y1 = h[idx], h[idx+1]
        zero = x0 - y0 * (x1 - x0) / (y1 - y0)
        zeros.append(zero)
        plt.plot([zero], [0], 'ro')  # Mark the zero

    plt.legend()
    plt.grid(True)
    plt.title('Graphical Method: f(x), g(x), and h(x) = f(x) - g(x)')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()

    print("The approximate zeros of h(x) are:", [round(z, 4) for z in zeros])

if __name__ == "__main__":
    plot_graphical_method(f, g)

Saída:
[[Resultado método gráfico.webp]]

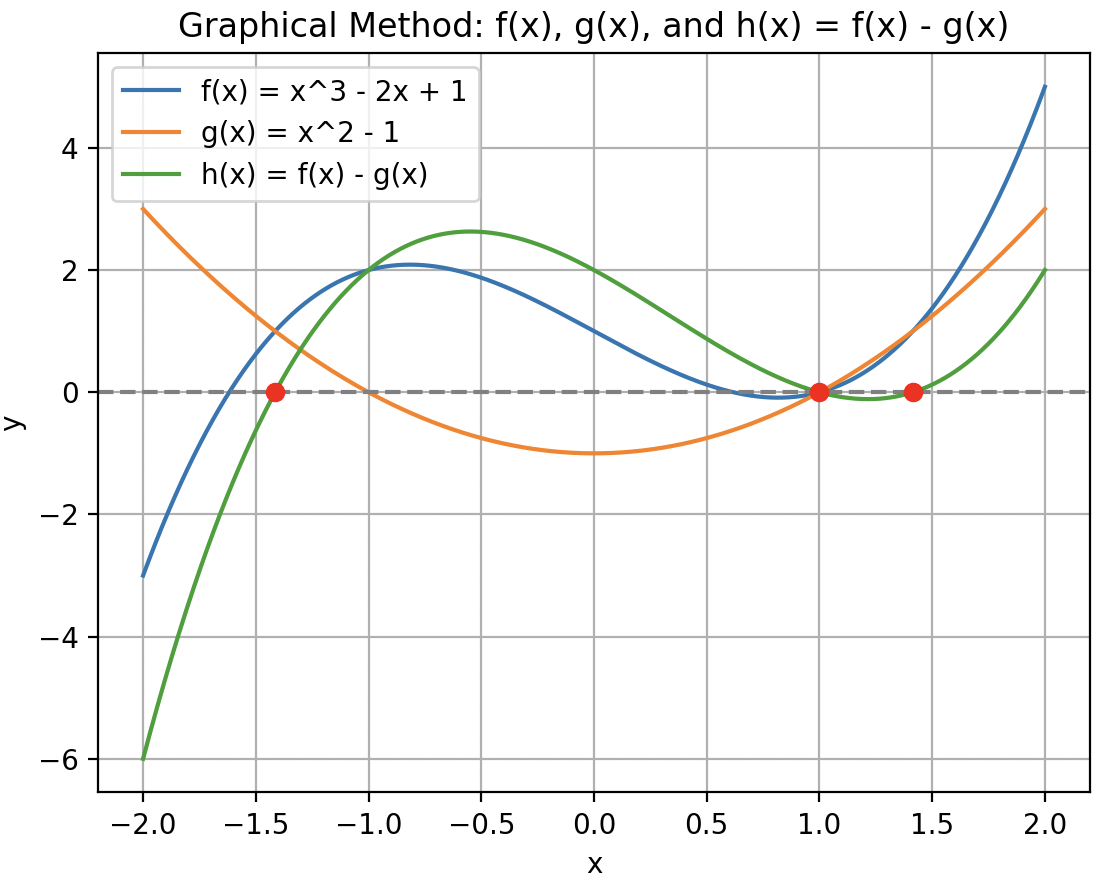
Limitações

O método gráfico é útil para obter uma visão geral rápida dos zeros de uma função, mas pode ser impreciso. Para obtenção de zeros com maior precisão, métodos numéricos como o método da bisseção ou Newton-Raphson são frequentemente utilizados em conjunto.

Este método gráfico fornece uma abordagem visual e intuitiva para entender a localização dos zeros de uma função, facilitando a compreensão do comportamento da função.